கடவுளும், சாத்தானும் (II)- ராஜ்சிவா

ஒரு உண்மையை முதலில் சொல்லிவிடுகிறேன். வாசகசாலையில் வாராவாரம் எழுத முடிவெடுத்தபோது, நான் வழமையாக எழுதும் அறிவியலை எழுதுவதில்லையென்றே தீர்மானித்திருந்தேன். மாறாக, மர்மங்களையும் (மிஸ்டரிகள்), அறிவியல் மர்மங்களையும், விந்தைகளையும், வியப்பான தகவல்களையும் ஒவ்வொன்றாகத் தனித்தனியாக உங்களுடன் பகிர்ந்துகொள்ளலாம் என்பதே என் நோக்க்கமாக இருந்தது. நான் எதைத் தொட்டுவிடக்கூடாது என்று நினைத்தேனோ, அதை என்னையறியாமலே தொட்டுவிட்டேன். ‘போல் டிராக்’ (Paul Dirac) என்னும் கணிதமேதையால் கண்டுபிடிக்கப்பட்ட ஒரு விந்தை முடிவைக் குறித்துச் சொல்வதற்காகவே ‘கடவுளும், சாத்தானும்’ என்று பெயரிட்டு ஆரம்பித்தேன். ஆனால், அதைச் சொல்ல ஆரம்பித்தபோதுதான் சற்று விளக்கிச் சொன்னால்தான் புரியுமென்ற நிலையில், கடந்த பகுதியை எங்கேயோ கொண்டுசென்றுவிட்டேன். அது என்னைக் கொண்டுபோய்க் கிணற்றில் தள்ளிவிட்டிருக்கிறது. இப்போது, அறிவியல் என்னும் சுழலில் என்னையும், உங்களையும் மாட்டியும் விட்டிருக்கிறது. கடந்த பகுதியில் நான் எழுதியவற்றிற்கு நீங்கள் கொடுத்த பெரிய ஆதரவையும், ஆர்வத்தையும் பார்த்தால், இதை முழுமையாகப் புரியும்படி சொன்னதன் பின்னரே நிறுத்த முடியும்போலத் தோன்றுகிறது. அதனால், கொஞ்சம் அறிவியலைத் தொட்டுச் செல்கிறேன், வாருங்கள். இந்தவகை அறிவியல் உங்களுக்குப் பிடித்திருந்தால், மேலும் வெவ்வேறு விசயங்களை எழுதுகிறேன். இல்லையெனில், முன்னர்போல எதையெழுத இருந்தேனோ, அதையே தொடர்கிறேன். முடிவெல்லாம் படிக்கும் உங்கள் கையில்தான். உங்களுக்காக எழுதுவதால், எது தேவையென்பதையும் நீங்களே முடிவு செய்யலாம். சரி இனி நாம் ஆரம்பிக்கலாம்.

குவாண்டம் இயற்பியல் ஆரம்பித்த காலமது. பாரம்பரிய இயற்பியலிலிருந்து, கோட்பாட்டு இயற்பியல் (Theoretical Physics) நோக்கி அறிவியல் வலதுபுறம் சிக்னல் போட்டு இடதுபுறம் திரும்பிக்கொண்ட காலம். பாரம்பரிய இயற்பியலுக்கும், கோட்பாட்டு இயற்பியலுக்கும் இடையில் அகப்பட்டுக்கொண்டவர் ஐன்ஸ்டைன் அவர்களே! குவாண்டம் இயங்கியலின் கோட்பாடுகளில் சிலவற்றை ஏற்றுக்கொள்ளவும் முடியாமல், தூக்கியெறியவும் முடியாமல் தவித்தார். ஆனால், இந்த குவாண்டம் இயங்கியலுக்கான விதையைப் போட்டவர்களில் முக்கியமானவர் அவர். அன்றிருந்த இளம் இயற்பியல் வல்லுணர்கள் அனைவருமே ஐன்ஸ்டைனால் வெளியிடப்பட்ட சார்புக் கொள்கைபால் வசீகரிக்கப்பட்டிருந்தார்கள் அதில் முக்கியமான ஒருவராக போல் டிராக் இருந்தார். 1928 ஆம் ஆண்டு, E=MC^2 என்னும் ஐன்ஸ்டைனின் சமன்பாட்டை முன்வைத்து அவரால் பல கணிதச் சமன்பாடுகள் உருவாக்கப்பட்டன. அடிப்படை நுண்துகள்கள் (Elementary particles), ஒளியின் வேகத்தில் இயங்கும்போது, எப்படியான நடவடிக்கைகளை மேற்கொள்கின்றன என்பதைக் கணிதச் சமன்பாடுகளின்மூலம் கணிக்க விரும்பினார். குறிப்பாக, ஒரு எலெக்ட்ரோன் ஒளிவேகத்தின் அண்மைக்குச் செல்லும்போது, எப்படி நடந்துகொள்கிறது என்பதை ஆராய்ந்தார். காரணம், அடிப்படை நுண்துகள்களில் எலெக்ட்ரோனும் ஒன்றாக இருந்தது. “அப்படியென்றால், புரோட்டோனும், நியூட்ரோனும்கூட அடிப்படை நுண்துகள்கள்தானா?” என்று அவசரப்பட்டு நீங்கள் கேட்டீர்களென்றால், “இல்லை” என்பதே பதில். “அது எப்படி?” என்று இப்போது பதில் சொன்னால், தலையெல்லாம் குழம்பிப்போய் மொபைலைத் தூக்கியெறிந்துவிட்டுச் சுவருடன் தலையை மோதிக்கொள்வீர்கள். அந்தப் பாவம் எனக்குத் தேவையில்லை. அனைத்தையும் சொல்கிறேன். மெல்ல மெல்ல நிதானமாகச் சொல்கிறேன். இப்போது, டிராக்குடன் பயணிப்போம்.

ஒளியின் வேகத்தில் எலெக்ட்ரோன் போன்ற அடிப்படை நுண்துகள்கள் பயணிக்கும்போது, அவற்றிற்கு என்ன நடக்குமென்று கணிக்க, டிராக் ஒரு கணிதச் சமன்பாட்டை உருவாக்கியபோதுதான் அந்தப் பிரச்சனை தோன்றியது. டிராக்குக்குப் பிரச்சனை ஒன்றும் புதிதல்ல. மிகக்கடுமையான கட்டுப்பாட்டுடன் இருந்த அப்பாவின் கீழ் வளர்ந்ததால், யாருடனும் எதுவும் பேசுவதில்லை அவர். மாபெரும் மௌனியாகவே டிராக் அதிக காலங்கள் வாழ்ந்திருக்கிறார். அப்பாவின் கட்டுப்பாட்டினால், தமையனார் தற்கொலை செய்திருந்ததும் பெரும் பின்னடைவாக இருந்தது. ஆனால், இயற்கையின் அதிசயமோ தனியானது. டிராக், ஹாக்கிங் போன்ற துயரர்களையே, சாதனையாலர்களாக மாற்றியிருக்கிறது. பேரண்டத்தின் மாபெரும் இரகசியங்கள் எல்லாம் இவர்களாலேயே விடுவிக்கப்பட வேண்டுமென்று இயற்கை என்றோ தீர்மானித்திருந்தது. எத்தனை பிரச்சனைகள் வந்தாலும், தடைகள் முன்னால் நின்றாலும், அவற்றை உடைத்தெறிந்து அறிவியலுக்கு அள்ளித் தந்தார்கள். ஆனாலும், டிராக்கின் கணிதச் சமன்பாட்டால் ஏற்பட்ட பிரச்சனை இனிமையானது. அறிவியலை அடுத்த கட்டத்திற்குத் தாவிப்பாய வைத்தது. எலெக்ட்ரோனின் ஆற்றலைக் கணிப்பதற்கான கணிதச் சமன்பாட்டை விடுவிக்கும்போது, டிராக்கிற்கு வந்த விடையானது வர்க்கமூலத்தில் (square root) இருந்தது. வர்க்கமூலம் (√) என்னும் கணித அடையாளத்தை நீங்கள் நிச்சயம் அறிந்திருப்பீர்கள். உதாரணமாக, 4 இற்கான வர்க்கமூலம் 2 என்பதாகும். 2X2=4 என்பதிலிருந்து, 4 இன் வர்க்கமூலம் 2 ஆகிறது. இவையெல்லாம் உங்களுக்கு ஏற்கனவே தெரிந்தவைதான். ஆனாலும், ஒருசிலர் மறந்திருக்கலாம் என்பதால் சொல்கிறேன். இப்படித்தான், போல் டிராக்கிற்கும் முடிவு வர்க்கமூலத்தில் கிடைத்தது. சிக்கலொன்றும் அதனுடன் சேர்ந்து வந்தது. அந்தச் சிக்கலே போல் டிராக்கிற்கு நோபல் பரிசையும் வாங்கிக் கொடுத்தது.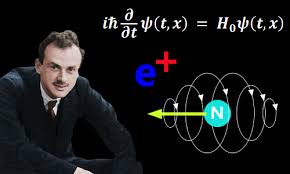சமன்பாட்டின் இறுதியில் வர்க்கமூலம் வந்தால், அதில் என்ன சிக்கல் வரமுடியும்?” என்றுதானே யோசிக்கிறீர்கள்? நிச்சயம் யோசிப்பீர்கள். காரணம் அறிவியலின் காதலர்களல்லவா நீங்கள். அந்தச் சிக்கல் என்னவென்று கணிதம் தெரிந்தவர்களுக்குத் தெரிந்திருக்கும். உண்மையில், ஒரு எண்ணின் வர்க்கமூலமாக ஒரேயொரு விடை வருவதில்லை. நேர், எதிரான இரண்டு விடைகள் கிடைக்கும். 4 இன் வர்க்கமூலம் 2 என்று சொன்ன்னேனல்லவா, அது தப்பில்லை. ஆனால் -2 என்னும் இன்னுமொரு விடையும் அதற்கு உண்டு. அதாவது, 2X2=4 என்பது மட்டும் விடையில்லை. -2X-2=4 என்பதும் அதற்கான விடைதான். 4 இற்கான வர்க்கமூலம், +2, -2 என்னும் இரண்டு விடைகளைக் கொண்டது. இப்படிக் கணிதத்திலுள்ள அனைத்து வர்க்கமூலங்களுக்கும் நேரான (+) விடையும், எதிரான (-) ஒரு விடையும் கிடைக்கும். உங்களுக்குப் புரிந்திருக்குமென்று நினைக்கிறேன். டிராக்கின் சமன்பாட்டில் வந்த வர்க்கமூலத்திற்கு ஒருவிடை கிடைத்தாலும், அதற்கு எதிரான இன்னுமொரு விடையும் இருந்தது. ஒரு துகளுக்கான ஆற்றலைப் பரிசோதிக்கும்போது, அதே துகள் எதிர் ஆற்றலைக் கொண்டதாகவும் இருக்கிறது என்று தெரியவந்தது. ஒரு துகளுக்குச் சமமான, ஆனால் எதிரான ஏற்றத்துடன் துகள் (Anti particle) இருக்கிறது என்று டிராக்கின் சமன்பாடு நிறுவியது. அதாவது, எலெக்ட்ரோனுக்கு எதிரான ஏற்றத்துடன், அதேபோன்ற எதிர் எலெக்ட்ரோன் (Anti electron) இருந்தே ஆகவேண்டுமென்று டிராக் கணித்துக் கொண்டார். பேரண்டத்திலுள்ள ஒவ்வொரு அடிப்படைத்துகளுக்கும் எதிரான இன்னுமொரு துகள் இருந்தே ஆகவேண்டுமென்ற முடிவுக்கு அவர் வந்தார்.

“அது எப்படி? இவர் மேசையில் உட்கார்ந்துகொண்டு எந்தவொரு ஆராய்ச்சியும் செய்யாமல், கணிதத்தால் ஒரு சமன்பாடு போடுவாராம். அந்தச் சமன்பாடு வர்க்கமூலத்தில் முடியுமாம். வர்க்கமூலத்துக்கு +, – என்ற இரண்டு விடைகள் வருமாம். அப்படி வந்ததால், துகள்களுக்கு எதிர்த்துகள்கள் பேரண்டத்தில் இருக்குமாம். என்ன விளையாடுகிறீர்களா? நீங்கள் கணிதத்தால் கணித்துச் சொன்னால், அவையெல்லாம் இயற்கையில் இருக்க வேண்டுமா என்ன? நீங்கள் அப்படியென்ன கடவுளா?” என்றுதான் இப்போது கேட்கத் தோன்றும். ஆனால், கணிதத்தாலேயே இயற்கையை அளந்தார்கள் மேதைகள் என்பது உண்மைதான். கண்ணால் காணாத ஒன்றை, இயற்கையில் அப்படியொன்று இருக்கிறது என்ற தகவலே இல்லாத ஒன்றை, கணிதம்மூலம் கணித்துச் சொல்வதென்பது எப்படிச் சாத்தியம்? இப்போது, ‘பிரிஸ்பா’ என்றொரு பூ, ஜெர்மனியில் இருக்கிறது. அருமையான மணம். மிக அழகாக இருக்கும் என்று நான் சொன்னால், நீங்கள் அதை எப்படிப் புரிந்துகொள்வீர்கள்? அதன் மணத்தையும், அழகையும் எப்படி உங்களால் கற்பனை செய்யமுடியும்? கண்ணால் காணாத ஒன்றைக் கணித்துச் சொல்வது என்பது ஆச்சரியமானதென்று புரிகிறதா? கருந்துளையென்ற ஒன்றைக் கேள்வியேபடாதபோதும், அப்படியொன்று இருக்கிறதென்று கணிப்பதும், அதைப் பின்னர் கண்டுபிடிப்பதும் எவ்வளவு மாபெரும் அதிசயம் சொல்லுங்கள்? வெறும் கணிதத்தினால் ஈர்ப்பலைகளையும் (Gravitational wave), ஹிக்ஸ் போஸான்களையும், எதிர்த்துகள்களையும் (Antimatter) கணித்துச் சொல்லி, அவை உண்மையென்று நிரூபிக்க்கப்படுவது எத்தனை ஆச்சரியம் சொல்லுங்கள்? அதுவரை ஒவ்வொரு துகளாகத் தேடிப்பிடித்து, வரிசைப்படுத்திவந்த ஆராய்ச்சியாளர்களுக்கு, ஒவ்வொரு துகளுக்கும் எதிர்த்துகள் இருக்கிறது என்ற டிராக்கின் முடிவினால், துகள்களின் எண்ணிக்கைகள் இரட்டிப்பாகிப் போயின.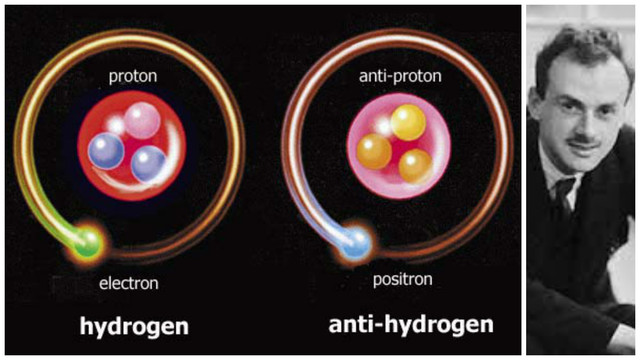துகள்கள் அனைத்துக்கும் எதிர்த்துகள்கள் இருக்கின்றன என்ற முடிவு எங்கு கொண்டுபோய் நம்மை விடும் தெரியுமா? எதிர்த்துகள்கள் இருந்தால், அவற்றால் உருவாக்கப்படும் அணுக்களாக, எதிர் அணுக்களும் இருக்கவேண்டும். எதிர் அணுக்கள் இருந்தால், அவை உருவாக்கும் எதிர் மூலக்கூறுகளும் இருக்கும். எதிர் மூலக்கூறுகள் இருந்தால், அவற்றால் உருவாக்கப்படும் எதிர்ப்பொருளும் இருக்கவேண்டும். ராஜ்சிவா இருந்தால், எதிர் ராஜ்சிவா இருப்பார். அதாவது ஆன்டி ராஜ்சிவா (Anti Rajsiva). ஆன்டி திரிஷா. ஆன்டி இந்… இப்போ நீங்கள் என்ன நினைக்கிறீர்கள் என்று எனக்குத் தெரியும். நான் அதைச் சொல்ல மாட்டேன். அவரின் பெயரையும் சொல்ல மாட்டேன். எதிர்த்துகள்கள் என்பவை அடிப்படையில் பெரிய மாற்றங்களைக் கொண்டவையல்ல. அவற்றின் மின்னேற்றம் (Electric charge) மட்டும் மாறியிருக்கும். எலெக்ட்ரோனின் ஏற்றம் எதிரேற்றம். அதனால். ஆன்டி எலெக்ட்ரோன் நேறேற்றம் உடையதாகக் காணப்படும். இதைத்தவிர எந்த மாற்றமும் இருக்காது. ஏற்றம் மாறுபடுவதால், அவற்றின் தன்மைகளுக்குப் பெரும்பாலும் வேறுபாடு இருக்காது. உதாரணமாகக் காந்தத்தின் வடமுனைக்கும், தென்முனைக்கும் உங்களால் என்ன மாற்றத்தைக் கண்டுகொள்ள முடியும்? அவை எதிரெதிரான ஏற்றங்களை மட்டும் கொண்டவை என்பதைத்தவிர. பூமியின் வடதுருவத்திற்கும், தென்துருவத்திற்கும் என்ன வித்தியாசம் உண்டு? ஒரு பாட்டரியின் மேல்முனைக்கும், கீழ்முனைக்கும் என்ன வித்தியாசம் காண்பீர்கள்? முகம் பார்க்கும் கண்ணாடியில் தெரியும் விம்பம்போல. அதில் நீங்கள் இதுவரை பார்ப்பது உங்கள் முகத்தைத்தான் என்று நம்பவில்லையா? அதுபோன்றவையே எதிர்த்துகள்களும். ராஜ்சிவாவுக்கும், ஆன்டி ராஜ்சிவாவுக்கும் அப்படியொன்றும் பெரிதாக வித்தியாசம் கிடையாது. ஆனாலும், டிராக்கின் முடிவைப் பலரால் ஜீரணிக்க முடியவில்லை. பெருங்குழப்பத்தில் இருந்தார்கள். உண்மையாகவே அப்படியான துகள்கள் உண்டாவெனத் தெரியாமல் தவித்தார்கள். இந்தக் குழப்பத்திற்கெல்லாம் சீக்கிரமே ஒரு முடிவு கிடைத்தது. அதுவும் நான்கே நான்கு ஆண்டுகளில்.1932ஆம் ஆண்டு, ’கார்ல் ஆண்டர்சன்’ (Carl David Anderson) என்னும் அமெரிக்க இயற்பியலாளர் செய்த பரிசோதனையொன்றில், எலெக்ட்ரோனுக்குச் சமமான ஆனால், + ஏற்றம்கொண்ட ஒரு துகள் கண்டுபிடிக்கப்பட்டது. ஆண்டர்சன் கண்டுபிடித்த அந்தத் துகள்தான் ‘பொசிட்ரோன்’ (Positron) என்பதாகும். டிராக் எதைக் கணித்திருந்தாரோ அதே துகள். இந்தப் பொசிட்ரோன் துகளே எலெக்ட்ரோனின் ஆன்டி எலெக்ட்ரோன் ஆகும். அதாவது, போல் டிராக் கணித்தது நூறுசதவீதம் சரியானதே என்று அனைவருக்கும் புரிந்துபோனது. அதன்பின்னர், படிப்படியாகப் பல எதிர்த்துகள்கள் கண்டுபிடிக்கப்பட்டன. அவையெல்லாம், முதல் பகுதியில் சொல்லியிருந்த துகள்மோதிகளின் மூலமாகக் கண்டுபிடிக்கப்பட்டன. அப்படியென்றால், இயற்கையில் இப்படியான எதிர்த்துகள்கள் இல்லையா? நம்மிடையே காணப்படும் அனைத்துத் துகள்களும், எதிர்த்துகள்களாக இல்லையே! அவை அனைத்தும் எங்கே? பிக்பாங் பெருவெடிப்பின்போது, துகள்களும், அவற்றிற்குச் சமமான எதிர்த்துகள்களும் ஒன்றாகவே உருவாகின என்றுதான் அறிவியலின் முடிவுகள் சொல்கின்றன. ஆனால், அந்த எதிர்த்துகள்கள் அனைத்தும் எங்கே? பேரண்டத்தின் உருவாக்கத்தில் நடந்தவொரு மர்மத்திற்கான பிரதான கேள்வி இது. இதற்கான சரியான பதில்கள் இன்றுவரை இல்லை. ஆனால், அவை எங்கே மாயமாகி இருக்க முடியும் என்பதற்கு மூன்றுவிதமான பதில்களை இயற்பியலாளர்கள் கொடுக்கிறார்கள்.

அவை என்னவென்று அடுத்த பகுதியில் சொல்கிறேன். அதிகம் எழுதினால், படிக்கும் உங்களுக்கும் ஒரு ஆயாசம் வந்துவிடும். நீண்ட கட்டுரைகள் அறிவியலுக்கு ஆபத்தானவை. அதனால், மெல்ல மெல்ல ஒவ்வொன்றாய் அறிந்துகொள்வோம். கட்டுரையை இடையில் முடித்ததால் சிலர் கோவப்படுவார்கள். அவர்களிடம் மன்னிப்பைக் கோருகிறேன். ஆனால், அன்டி ராஜ்சிவாவும், அன்டி திரிஷாவும் எங்கே போனார்கள் என்று அடுத்த பகுதியில் நிச்சயம் சொல்கிறேன்.

தொடரும்…